This section yields analytical insight into the above strategy with a new Post-Keynesian Stock-Flow Consistent (PK-SFC) model in the spirit of Godley and Lavoie (2012)Footnote 11. The model is comprised of 106 accounting and behavioral equations interlocked in a sectoral transaction matrix, as well as one ‘hidden’ equation implied by all the other. The model contributes to the SFC modeling literature by including local complementary currencies and new resilience metrics.
The transaction flows matrix
The model’s transaction matrix is shown in Table 2. This transaction matrix ensures that all flows and stock readjustment are interlocked in a watertight accounting structure, while integrating the real and financial sides of the economy. The matrix describes a simplified economy with five institutional sectors: households, production firms (divided into the LCC and the euro sector), a banking sector and a Central Bank. There is no government nor public sector in the model. This assumption means that money is emitted through bank loans (in the form of new deposits).
Each economic transaction is double-sided: one sector’s income is another sector’s spending, and one sector’s asset is another sector’s liability. Annual change to the stock of assets and liabilities held by each sector (columns) result from the budget constraint of each individual sector, defined by annual flows of income and spending (rows). This approach ensures a full integration of the real and financial sides of the economy. Following SFC modelling convention, a (+) sign indicates a source of funds while a (–) sign indicates a use of funds.
Column 1 shows the budget constraint of households. Households receive income as wages (W), profits redistributed by firms (F) and banks (FB), and interests on their euro (\({r}_{d,m\left(-1\right)}{M}_{h,m,s\left(-1\right)}\)) and local complementary currency deposits (\({r}_{d,{lcc}\left(-1\right)}{M}_{h,{lcc},s\left(-1\right)}\)). Households spend their income on consumption expenditures in euros (Cm) and in complementary currency (\({C}_{{lcc}}\)). At the end of each period, excess of income over spending accumulates in stocks of banking deposits, which households hold both in euros (\(\triangle {M}_{m}\)) and in local complementary currency units (\(\triangle {M}_{{lcc}}\)).
Columns 2 and 3 divide the production firm sector’s transactions into a current and capital account. It amalgamates the LCC eligible sector (where both euros and LCCs can circulate) and the non-eligible sector (where only the euro can circulate). Column 2 shows the receipts and outlays of production firms. Firms receive payment flows on their sales of final goods in euros (\({C}_{m}\)) and in local complementary currencies (\({C}_{{lcc}}\)), as well as their sales of capital goods (in euros (\(I\)) and in local complementary currencies (\({I}_{{lcc}}\))). Firms pay wages to households (W) (in euros and LCCs) and interest on their loans in euros (\({r}_{l,m\left(-1\right)}{L}_{m,-1}\)) and in local complementary currencies (\({r}_{l,{lcc}\left(-1\right)}{L}_{{lcc},-1}\)) and set aside funds for depreciation allowances (DA) – also decomposed into euros and LCC allowances.
Column 3 shows firms’ capital expenditures, which are financed by depreciation allowances (DA), new loans in euros (\(\triangle {L}_{d,m}\)) and in local complementary currencies (\(\triangle {L}_{d,{lcc}}\)). In our simple framework, profits (F) are fully redistributed to households (in euros and LCCs).
Columns 4 and 5 show the current account and the capital account of banks. As shown in column 4, banks receive interest payments on loans in euros (\({r}_{l,m\left(-1\right)}{L}_{m,-1}\)) and local complementary currencies (\({r}_{l,{lcc}\left(-1\right)}{L}_{{lcc},-1}\)) and pay interests on deposits in euros (\({r}_{d,m\left(-1\right)}{M}_{h,m,s\left(-1\right)}\)) and in local complementary currencies (\({r}_{d,{lcc}\left(-1\right)}{M}_{h,{lcc},s\left(-1\right)}\)). Column 5 shows that new deposits in euros (\(\triangle {M}_{m})\) and in complementary local currencies (\(\triangle {M}_{{lcc}}\)) are recorded on the liability side of banks’ balance sheets. Bank assets include loans in euros \((\triangle {L}_{d,m}\)), in local complementary currencies \((\triangle {L}_{d,{lcc}})\), and high-powered money (\(\triangle A\)). The latter is emitted through the ex-post rediscounting of LCC loan impact certificates (φ). The difference between bank’s interest income from loans and interest payments and deposits, plus annual additions in reserve assets obtained through loan rediscounting, constitutes their profit, which is entirely redistributed to the household sector (in euros and LCCs) (FB). Column 6 shows the capital account of the Central Bank. In this simplified setting, the Central Bank’s only liability is the high-powered money (reserve currency) that it issues (\(A\)), in exchange for impact certificates (φ). These impact certificates measure a net contribution to SDGs, and therefore do not appear as a liability for any sector.
Behavioral equations
We begin with the definition of total gross production (GDP). GDP (Y) is the sum of all expenditures on goods and services, including consumption \((C)\) and investment goods \({(I}_{f,s})\) (Eq. 1.1). GDP is decomposed into euro \({(Y}_{m})\) and LCC \({(Y}_{{lcc}})\) spending (Eqs. 1.2 and 1.3)
$${Y}_{m}={C}_{m}+{(I}_{f,s}-{L}_{s,{lcc}})$$
(1.2)
$${Y}_{{lcc}}=Y-{Y}_{m}$$
(1.3)
GDP also corresponds to the sum of factor payments, which includes the wage bill (WB), production firms’ profits (F), banking profits (FB), and the depreciation and amortization funds (DA) that firms set aside to replace used-up capital. The model’s accounting closure shall ensure that Eqs. (1.4) and (1.1) are equal in all states of the model.
$$Y={WB}+F+{FB}+{DA}$$
(1.4)
Total personal disposable income (YD) is equal to GDP net of depreciation and amortization funds (Eq. 2.1). It is also equal to the sum of euro disposable income (\({{YD}}_{m})\) and LCC disposable income \({({YD}}_{{lcc}})\) (Eqs. 2.2 and 2.3).
$${{YD}}_{m}={Y}_{m}-{{DA}}_{m}$$
(2.2)
$${{YD}}_{{lcc}}={YD}-{{YD}}_{m}$$
(2.3)
The wage bill (WB) is a fixed proportion \((w)\) of GDP. It is decomposed into euro wages \({({WB}}_{m})\) and LCC wages \({({WB}}_{m})\) (Eqs. 3.1 to 3.3).
$${{WB}}_{{lcc}}=w.{Y}_{{lcc}}$$
(3.2)
$${{WB}}_{m}={WB}-{{WB}}_{{lcc}}$$
(3.3)
Total household consumption is the sum of euro and LCC consumption. Households determine the level of euro consumption by drawing on their disposable income and on the stock of banking deposits which they inherit from the previous period. Macroeconomic consumption (in euros) depends on an autonomous incompressible component (\({\alpha }_{0}\)), on disposable income \(({{YD}}_{m})\) (according to a factor \({\alpha }_{1}\)) and euro banking deposits \({(M}_{h,m,s-1})\) (according to a factor \({\alpha }_{2}\, < \,{\alpha }_{1}\)). Given that households hold LCC mostly for consumption purposes, the propension to draw from LCC income and deposits depends on a single factor \({\alpha }_{3}\) (Eqs. (4.1) to (4.3)). In the baseline simulation, \({shock}=0\), which means that there is no LCC consumption expenditure in the economy (Eq. (4.3)).
$$C={C}_{m}+{C}_{{lcc}}$$
(4.1)
$${C}_{m}={\alpha }_{0}+{\alpha }_{1}\left({{YD}}_{m,-1}\right)+{\alpha }_{2}{(M}_{h,m,s-1})$$
(4.2)
$${C}_{{lcc}}={shock}\times \left({\alpha }_{0,l}+{\alpha }_{3}\left({{YD}}_{{lcc},-1}+{M}_{h,{lcc},s-1}\right)\right)$$
(4.3)
We now describe the budget constraint and the portfolio behavior of households. We follow Godley and Lavoie (2012, ch.4) and model households’ demand for liquid assets (which includes sight deposits and LCCs) as a buffer, which varies according to unexpected variations in household income. At the end of each year, whatever total disposable income \(({YD})\) not spent on consumption \((C)\) is added to households’ total financial wealth \({M}_{h}\) (5.1). Households’ euro-denominated holdings are determined using similar principles (Eq. 5.2). Households’ LCC holdings is determined using an accounting criterion (Eq. (5.3)).
$${\triangle M}_{h}={M}_{h}-{M}_{h-1}={YD}-C$$
(5.1)
$${\triangle M}_{h,m}={{YD}}_{m}-{C}_{d,m}$$
(5.2)
$${\triangle M}_{h,{lcc}}={\triangle M}_{h}-{\triangle M}_{h,m}$$
(5.3)
The model contains three financial assets: savings account deposits, sight deposits (both in euros) and LCC holdings. Households’ demand for savings account deposits \(({\triangle M}_{h,m,d})\) depends on their expected total financial wealth \(({M}^{e})\) and expected euro disposable income (\({{YD}}^{e})\).
Households wish to hold a given proportion \(({\lambda }_{0})\) of their expected wealth in the form of savings account deposits, and this proportion increases with their expected disposable income, according to a parameter \({\lambda }_{1}\, > \,0\) (Eq. (6.1)). Households’ targeted holdings of sight deposits \(({\triangle M}_{h,h,d}\)) can then be determined with an accounting closure criterion, as shown in Eq. (6.2). Finally, whatever amount of LCCs is not spent at the end of the year is simply added to the stock of LCC holdings (6.3). In the baseline scenario, \({shock}=0\) so that households do not allocate any share of their wealth in LCCs. The supply of financial assets is equal to demand (Eqs. (6.4) to (6.6)).
$$\frac{{\triangle M}_{h,m,d}}{{M}^{e}}={\lambda }_{0}+{\lambda }_{1}\frac{{{{YD}}_{m,-1}^{e}}^{}\,}{{M}_{h}}$$
(6.1)
$${\triangle M}_{h,h,d}={{\triangle M}_{h,m}-\triangle M}_{h,m,d}$$
(6.2)
$${M}_{h,{lcc},d}={shock}\times \left({M}_{{lcc},-1}+{{YD}}_{{lcc}}-{C}_{{lcc}}\right)$$
(6.3)
$${\triangle M}_{h,m,s}={\triangle M}_{h,m,d}$$
(6.4)
$${\triangle M}_{h,h,s}={\triangle M}_{h,h,d}$$
(6.5)
$${\triangle M}_{h,{lcc},s}={\triangle M}_{h,{lcc},d}$$
(6.6)
Expected wealth \({(M}^{e})\) is the mirror of realized wealth (equation (5)) in the realm of expectations. It is defined in Eq. (7):
$${M}^{e}={M}_{h,-1}+\left({{YD}}^{e}-C\right)$$
(7)
Expected euro disposable income (\({{{YD}}_{m}^{e}}^{}\)) is modeled as a weighted average of its past and expected value (Godley and Lavoie 2012, p.291) (Eq. (8)).
$${{{YD}}_{m}^{e}}^{}={\varepsilon {YD}}_{m,-1}+\left(1-\varepsilon \right){{YD}}_{m,-1}^{e}$$
(8)
Let us now look at the production sector. In both the euro and LCC-denominated sectors, the demand for investment \({(I}_{f,m,d}\) and \({I}_{f,{lcc},d}\), respectively) is based on the partial accelerator model and has two components: the first is forward-looking and adjusts partially \(\left(\gamma\, < \,1\right)\) to the discrepancy between the targeted capital stock \({(K}^{T})\) and the stock of productive assets \({(K}_{-1}\)) inherited from the previous period. The second component consists in expenditure required to replace the used-up machines (DA) (equation (11)):
$${I}_{f,m,d}=\gamma \left({K}_{m}^{T}-{K}_{m,-1}\right)+{{DA}}_{m}$$
(11.1)
$${I}_{f,{lcc},d}=\gamma \left({K}_{{lcc}}^{T}-{K}_{{lcc}-1}\right)+{{DA}}_{{lcc}}$$
(11.2)
In both sectors, depreciation and amortization funds (DA) are defined as a fixed proportion \((0\,< \,\delta \,<\, 1)\) of the stock of capital \(({K}_{-1})\) that firms hold at the beginning of the fiscal year (equation (12)).
$${{DA}}_{m}=\delta {K}_{m-1}$$
(12.1)
$${{DA}}_{{lcc}}=\delta {K}_{{lcc}-1}$$
(12.2)
Entrepreneurs have adaptive expectations and index the targeted capital stock \({(K}^{T})\) to total macroeconomic income achieved in the previous period (Eq. (13.1)). However, LCC sector entrepreneurs adjust their capital stock target in reference to LCC-denominated income (i.e. to the size of the LCC community) (Eq. (13.2)).
$${K}_{m}^{T}=\kappa {Y}_{-1}$$
(13.1)
$${K}_{{lcc}}^{T}={\kappa Y}_{{lcc}-1}$$
(13.2)
The stock of productive capital \((K)\) is equal to the stock inherited from the previous period \({(K}_{-1})\) net of depreciation allowances \((\delta {K}_{-1})\), plus newly acquired capital \({(I}_{f,s})\) (equation (14)). It is decomposed into euro and LCC denominated capital (equation (14)).
$${{K}_{m}}^{}=\left(1-\delta \right){K}_{m,-1}+{I}_{f,m,s}$$
(14.1)
$${{K}_{{lcc}}}^{}=\left(1-\delta \right){K}_{{lcc},-1}+{I}_{f,{lcc},s}$$
(14.2)
$$K={K}_{m}{+K}_{{lcc}}$$
(14.3)
The above framework ensures that the introduction of LCCs affects both firms’ investment behavior and the stock of productive capital. Sectoral balance sheets track the euro and LCC components of physical capital assets, amortization funds, capital stock targets, financial wealth and income flows.
The profits of both banks and productive firms are fully distributed as dividends to the household sector. Thus, firms finance net investment through new bank loans. Money creation results from the interplay between firms’ productive bets and banks’ lending decisions. The demand for new loans \((\triangle {L}_{d})\) equals the net demand for investment, i.e. the difference between gross demand for investment \({(I}_{f,d})\) and set-aside amortization funds (\({DA}\)) in euros and LCCs (Eqs. (16.1) to (16.3)). In the baseline simulations, \({shock}\) is set to zero and there is no demand for credit in LCCs (Eq. (16.2)).
$$\triangle {L}_{f,d,m}={I}_{f,d,m}-{{DA}}_{m}$$
(16.1)
$$\triangle {L}_{f,d,{lcc}}={shock}\times ({I}_{f,d,{lcc}}-{{DA}}_{{lcc}})$$
(16.2)
$$\triangle {L}_{f,d}=\triangle {L}_{f,d,m}+\triangle {L}_{f,d,{lcc}}$$
(16.3)
The afflux of money is described in Eqs. (17.1) to (17.6). Banks screen euro loans applications based on the expected creditworthiness of borrowers \((\rho )\) (Eq. (17.1)). The supply of LCC loans equals demand from LCC firms, plus a fraction (which we set to one) of the rejected applications for euro-loans.
We assume that banks reject SDG-contributing, yet non-creditworthy demand for investment. Yet, these investments carry a positive SDG impact, which banks can rediscount at the Central Bank. In the baseline simulations \({shock}\) is set to zero so that euro-investment is constrained and no LCC credit takes place (Eq. (17.2)). Equations (17.3) to (17.6) are accounting equations defining the stock of loans and annual total, euro and LCC investment, respectively.
$${\triangle L}_{f,s,m}={L}_{f,d,m}(1-\rho )$$
(17.1)
$${\triangle L}_{f,s,{lcc}}={shock}\times ({L}_{f,d,{cc}}+(\rho {L}_{f,d,m})$$
(17.2)
$${L}_{s}={L}_{f,s,m}+{L}_{f,s,{lcc}}$$
(17.3)
$${I}_{f,s,m}={\triangle L}_{f,s,m}+{{DA}}_{m}$$
(17.4)
$${I}_{f,s,{lcc}}={\triangle L}_{f,s,{lcc}}+{{DA}}_{{lcc}}$$
(17.5)
$${I}_{f,s}={I}_{f,s,m}+{I}_{f,s,{lcc}}$$
(17.6)
At each period, productive firms’ profits are equal to the difference between GDP and other factor payments (using the income definition for GDP) (Eq. (18.1)). Profits are broken down into euro and LCC profits (Eqs. (18.2) and (18.3)) here
$$F=Y-{WB}-{FB}-{DA}-{r}_{d,m,-1}{M}_{h,m,s,-1}-{r}_{d,{lcc},-1}{M}_{h,{lcc},s-1}$$
(18.1)
$${F}_{{lcc}}={Y}_{{lcc}}-{{WB}}_{{lcc}}-{{FB}}_{{lcc}}-{{DA}}_{{lcc}}-{r}_{d,{lcc},-1}{M}_{h,{lcc},s-1}$$
(18.2)
$${F}_{m}={Y}_{m}-{{WB}}_{m}-{{FB}}_{m}-{{DA}}_{m}-{r}_{d,m,-1}{M}_{h,m,s,-1}$$
(18.3)
Banks charge different interest on loans issued in euros \(\left({r}_{l,M}\left({L}_{s,m,-1}\right)\right)\) and LCC \(\left({r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)\right)\). Their profit is the interest spread, plus any new reserve assets \({\triangle A}_{s}\) obtained from the Central Bank through impact rediscounting. Rediscounting implies that LCC loans are less risky from the banks’ perspective. We thus set \({r}_{l,{lcc}}\) < \({r}_{l,M}\) (see Table A2 in the appendix) (Eq. (19)).
$$\begin{array}{l}{FB}={r}_{l,M}\left({L}_{s,m,-1}\right)+{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)+\,{\triangle A}_{s}\\\qquad\quad-\,{r}_{d,M}\left({M}_{s,m,-1}\right)-{r}_{d,{lcc}}\left({M}_{{lcc},-1}\right)\end{array}$$
(19)
We now turn to the Central Bank’s rediscounting policy. As discussed, impact rating agencies compute the annual SROI of the circulation of the LCC deposits emitted through bank loans at the previous period. Banks obtain an annual flow of impact certificates \(({\varphi }_{s}\)) (Eqs. (20.1) and (20.2)).
$${\varphi }_{d}=\left(1+{SROI}\right){L}_{s,{lcc},-1}$$
(20.1)
$${\varphi }_{s}={\varphi }_{d}$$
(20.2)
Banks swap these impact certificates for new reserve assets at the Central Bank.
The Central Bank applies a haircut \((\tau )\) in this transaction (Eq. (21.2). The haircut rate is a discretionary yet, as shown in Eq. (22), we model it as an endogenous variable. The haircut rate depends on two components: its past value, and the product of normally distributed random shocks \((\varepsilon\)) (reflecting the evolution of the monetary policy framework) and first-differenced impact ratings. This means that an increase in the SDG performance of LCC loans shall lead Central Banks to decrease of the haircut rate, subject to any other random shock \((\varepsilon\)). We set the starting value of the haircut rate at 4.5%, which corresponds to the valuation markdown which the ECB applied to asset-backed securities at the time of writing (European Central Bank 2022a, b).
$${H}_{s}={A}_{d}$$
(21.1)
$${A}_{d}=(1-\tau ).{\varphi }_{s,-1}$$
(21.2)
$$\tau ={\tau }_{-1}+\varepsilon \varDelta {SROI}$$
(22)
Interest rates are set as exogenous parameters. SROI impact ratings of LCC deposits are modeled as a stochastic process, with annual random innovations \(\xi\) following a Laplace distribution around a mean of 15% (Walter 2020) (Eqs. (23.1) to (23.5)).
$${r}_{l,m}={\overline{{r}_{l,m}}}$$
(23.1)
$${r}_{l,{lcc}}={\overline{{r}_{l,{lc}}}}$$
(23.2)
$${r}_{c,m}={\overline{{r}_{d,m}}}$$
(23.3)
$${r}_{d,{lcc}}={\overline{{r}_{d,{lcc}}}}$$
(23.4)
$${SROI}=\overline{{SROI}}+\xi$$
(23.5)
The supply of money \({(M}_{h})\) (in euros and local complementary currency) held by households is modeled in Eq. (5.1). New loans (in euros and local complementary currency) recorded in banks’ balance sheets are given by Eq. (17.3). Although the supply and demand of bank deposits depend on different process, they shall be equal in all states of the model by virtue of its accounting consistency (i.e. without any equilibrium condition being imposed). Equation (24) is therefore the model’s hidden equation. This feature of the model qualifies it as a post-Keynesian SFC model insofar as money creation is entirely driven by the behavior of banks and productive firms. The model assumes no multiplier mechanism that would run from the reserves to new deposit creation by private banks (Bank of England 2014; Wray 2012; Ehnts 2017).
$${\triangle M}_{h}={\triangle L}_{s}$$
(24)
Finally, the model features a resilience block based on Ulanowicz et al. (2009). This requires us to introduce the following definitions. Let \({T}_{i.}\) represent the expenditure of each sector i to any other sector; \({T}_{.j}\) is the net income of sector j from any other sector; and \({T}_{{ij}}\) the expenditure of any sector i to any sector j. The sum of all net transfers of money between sectors i and j is \({{T}_{..}=\sum _{{ij}}T}_{{ij}}\). We focus on private sector transactions only, and consider households (h), banks (b) and productive firms (f).
Equation (24.1) shows that the expenditure of household to other units \({(T}_{h.})\) equates consumption spending to the firm sector, in the legal tender and in LCCs \({(C}_{m}+{C}_{{lcc}})\). Equation (24.2) shows that the income of households from other sectors \({(T}_{.h})\) is the sum of wages and distributed profits paid by productive firms in the legal tender and in LCCs \({({WB}}_{m}+{{WB}}_{{lcc}}+{F}_{m}+{F}_{{lcc}})\), interest payments and distributed profits from banks \(\left({r}_{l,M}\left({L}_{s,m,-1}\right)+{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)+{FB}\right)\).
Equation (24.3) shows that the expenditure of productive firms to other units \({(T}_{f.})\) is the sum of net investment spending \({(\triangle L}_{s,m}+{\triangle L}_{s,{lcc}})\), wages and profits paid to the household sector \({({WB}}_{m}+{{WB}}_{{lcc}}+{F}_{m}+{F}_{{lcc}})\), and interest paid to the banking sector \(\left({r}_{l,M}\left({L}_{s,m,-1}\right)+{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)\right)\).
Equation (24.4) shows that the net income of productive firms from other units \({(T}_{.f})\) is the sum of the new loans issued by the banking sector \({(\triangle L}_{s,m}+{\triangle L}_{s,{lcc}})\) and household consumption \({(C}_{m}+{C}_{{lcc}})\).
Equation (24.5) defines the banking sector’s expenditure \({(T}_{b.})\) to other units as the sum of new loans issued to productive firms \({(L}_{s,m}+{L}_{s,{lcc}})\), interest payments, and profits distributed to households \(\left({r}_{d,M}\left({M}_{s,m,-1}\right)+{r}_{d,{lcc}}\left({M}_{{lcc},-1}\right)+{FB}\right)\). Equation (24.6) measures the income of the banking sector \({(T}_{.b})\) as the sum of the interest payments received from productive firms \(\left({r}_{l,M}\left({L}_{s,m,-1}\right)+{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)\right)\).
$${T}_{h.}={C}_{m}+{C}_{{lcc}}$$
(25.1)
$${T}_{.h}={{WB}}_{m}+{{WB}}_{{lcc}}+{F}_{m}+{F}_{{lcc}}+{r}_{d,M}\left({M}_{s,m,-1}\right)+{r}_{d,{lcc}}\left({M}_{{lcc},-1}\right)+{FB}$$
(25.2)
$$\begin{array}{ll}{T}_{f.}={L}_{s,m}+{L}_{s,{lcc}}+{{WB}}_{m}+{{WB}}_{{lcc}}+{r}_{l,M}\left({L}_{s,m,-1}\right)\\\qquad\quad+\,{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)+{F}_{m}+{F}_{{lcc}}\end{array}$$
(25.3)
$${T}_{.f}={L}_{s,m}+{L}_{s,{lcc}}+{C}_{m}+{C}_{{lcc}}$$
(25.4)
$${T}_{b.}={L}_{s,m}+{L}_{s,{lcc}}+{r}_{d,M}\left({M}_{s,m,-1}\right)+{r}_{d,{lcc}}\left({M}_{{lcc},-1}\right)+{FB}$$
(25.5)
$${T}_{.b}={r}_{l,M}\left({L}_{s,m,-1}\right)+{r}_{l,{lcc}}\left({L}_{s,{lcc},-1}\right)$$
(25.6)
Defining the sum of all net transfers of money between units i and j as \({{T}_{..}=\sum _{{ij}}T}_{{ij}}\), the occurrence probability of each transaction is equal to its observation frequency:
$${p}_{{ij}}=\frac{{T}_{{ij}}}{{T}_{..}}\,;\,{p}_{i.}=\frac{{T}_{i.}}{{T}_{..}}{\rm{;}}{p}_{.j}=\frac{{T}_{.j}}{{T}_{..}}\,$$
Following Ulanowicz et al. (2009), we can now define the evolutionary capacity of the economic system as \(C=A+\Phi\). Each term is defined in Eqs. (26.1) to (26.3):
$$C=-\mathop{\sum}\limits_{{ij}}{T}_{{ij}}\log \left(\frac{{T}_{{ij}}}{{T}_{..}}\right)$$
(26.1)
$$A=\mathop{\sum}\limits_{{ij}}{T}_{{ij}}\log \left(\frac{{T}_{{ij}}{T}_{..}}{{T}_{i.}{T}_{.j}}\right)$$
(26.2)
$$\Phi =-\mathop{\sum}\limits_{{ij}}{T}_{{ij}}\log \left(\frac{{T}_{{ij}}^{2}}{{T}_{i.}{T}_{.j}}\right)$$
(26.3)
Letting \(a=\frac{{\rm{A}}}{C}\), and applying a Boltzmann transformation yields the system’s fitness for evolution metric F (Eq. (27)):
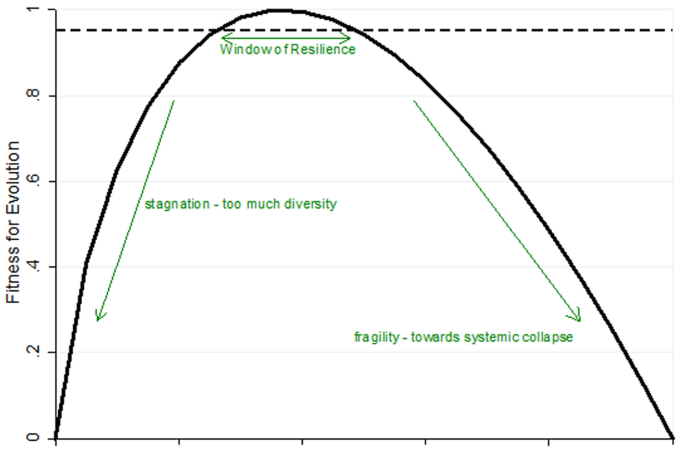
Where k is a positive scalar set to 2.71. As discussed in Section 2.2., when \(a=\)1, \(F\) tends to zero due to a lack of resilience. When \(a\,=\,0\), \(F\) also tends to zero due to a lack of ascendency. \(F\) increases for intermediate values of \(a\) and peaks when \(a=\frac{1}{e}\) = 0.36 (see Fig. 1).