Urban form and structure explain variability in spatial inequality of property flood risk among US counties
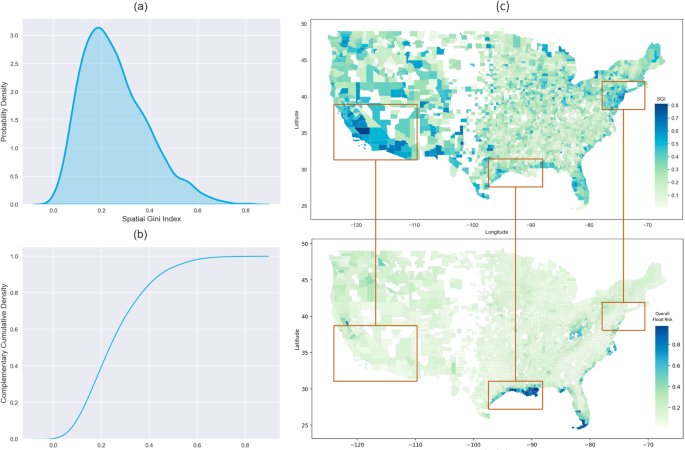
Definition and data for spatial inequality of property flood risk
Spatial inequality of property flood risk refers to the uneven distribution of flood risk across different geographic areas. It reflects the extent to which certain areas exhibit a higher likelihood of experiencing flood damage to properties than others. This discrepancy arises from a complex interplay of factors, encompassing physical, environmental, and socio-economic elements. While it is widely accepted that various factors, such as hydrology and land topography, influence flood risk8,9,10, it is crucial to emphasize that our primary focus in this paper is on how urban form and structure impact this inequality. The significance of urban form and structure in shaping the spatial distribution of flood risk in cities is increasingly gaining recognition11,12.
The raw dataset of property flood risk was obtained from Flood Factor Score, a model created by First Street Foundation33. The Flood Factor model assesses the flood risk of every property in an area and assigns it a risk score from 1 to 10. A score of 1 indicates a low chance of flooding within the next 30 years; a score of 10 indicates a high chance of flooding. The methodology employed by the Flood Factor model involves the integration of property-level data (i.e., elevation, precipitation, environmental changes over time, and community protection initiatives), overlaying building footprints, and applying flood hazard layers to calculate the probability of the maximum depth of floodwater reaching a given property. It’s important to note that this dataset encompasses all types of properties in a given area. Also, our dataset has already taken the variations of various types of properties into account during the calculations, incorporating factors such as property type, year of construction, structure, height, and whether the property is situated within a floodplain33.
SGI is a measure of spatial inequality. It is calculated as the area difference between a perfectly equal distribution and the actual distribution34,35. An SGI of 0 represents a perfectly equal distribution of the feature of interest and 1 would describe a distribution where different areas have different values of the feature of interest34. In this study, SGI captures the spatial heterogeneity of property flood risk in a county. We calculated the percentage of property flood risk for each county by dividing the number of properties with Flood Factor score larger than six to the total number of properties, denoted here by \({x}_{i}\). The entropy-based SGI is given by36:
$${SGI}=\frac{{\sum }_{i=1}^{N}{\sum }_{j=1}^{N}{w}_{{ij}}\left|{x}_{i}-{x}_{j}\right|+(1-{w}_{{ij}})\left|{x}_{i}-{x}_{j}\right|}{2{n}^{2}\left\langle x\right\rangle }$$
(1)
where N is the number of neighborhoods, and \(\left\langle x\right\rangle =\frac{1}{N}{\sum }_{i}{x}_{i}\) is the mean of the variable of interest. The spatial weight \({w}_{{ij}}\) is defined according to the adjacency matrix A where \({w}_{{ij}}\) = 1 if two areas are neighbors, and 0 otherwise. The diagonal elements \({w}_{{ii}}\) = 0 as defined in A and W corresponds to the sum of all weights.
Definition and data for urban form features
GDP
To estimate the status of the economic development of the county, we adopted the 2019 data of gross domestic product for each county. The data are provided by the Bureau of Economic Analysis in the US Department of Commerce37.
Population density
The population size was obtained from the 2020 race and ethnicity data from US Census Bureau38. We calculated the population density at the county level by dividing the total population of the county by its land area. Land area data was also obtained from the US Census Bureau39.
Minority segregation and income segregation
Urban segregation refers to the physical and social separation of different racial, ethnic, and socioeconomic groups within a city40. This separation can take many forms, including minority segregation and income segregation. One of the key consequences of urban segregation is that it often leads to unequal distribution of resources, as well as increased exposure to environmental hazards such as flooding41,42.
In this study, we adopted the Dissimilarity Index (DI) to evaluate minority segregation and income segregation. The DI is a measure of spatial segregation that indicates the extent to which two groups are evenly distributed across different areas, which ranges from 0 (indicating perfect evenness) to 1 (indicating complete separation)43,44. We calculated the DI based on the proportion of minority population (for minority segregation) and the proportion of low-income population (for income segregation) at the census tract level relative to the county level45:
$${DI}=\frac{1}{2}\mathop{\sum }\limits_{i=1}^{n}\left|\frac{{x}_{i}}{X}-\frac{{y}_{i}}{Y}\right|$$
(2)
where \({x}_{i}\) is the minority population (or low-income population) in the smaller geographical unit; \(X\) is the minority population (or low-income population) in the larger geographical unit. \({y}_{i}\) is the reference population in the smaller geographical unit; \(Y\) is the reference population in the larger geographical unit. In our study, smaller geographical unit refers to census tract level and the larger geographical unit refers to county level.
For minority segregation, we collected the racial population data from the 2020 race and ethnicity data from the US Census Bureau38. The primary racial groups in this study are non-Hispanic White, non-Hispanic Black, and non-Hispanic Asian residents. Non-Hispanic populations are selected because White, Black, or Asian populations can be mutually selective from Hispanic populations. The method of this kind of analysis is consistent with those frequently adopted by high-impact research works25,46,47. We considered the non-Hispanic Black, and non-Hispanic Asian as the minority population and non-Hispanic White as the reference population.
For income segregation, we extracted median income data from the 2020 American Community Survey48. This study used the 5-year estimates of median income due to the broader coverage of areas, larger sample size, and higher precision, making the data more reliable than 1-year and 3-year estimates. We used the quantile income groups of a county (Q1 to Q4) to indicate income levels with Q1/Q2 representing low-income groups and Q3/Q4 represent high-income groups, respectively.
Definition and data for urban structure features
POI density
To capture the distribution of physical facilities, we adopted the 6.5 million active POI data in the US from SafeGraph49. The dataset includes basic information about POIs, such as POI IDs, location names, geographical coordinates, addresses, brands, and North American Industry Classification System (NAICS) codes to categorize POIs. The NAICS code is the standard used by federal statistical agencies in classifying business establishments50. In this study, we selected ten essential types of POIs that are closely relevant to human daily lives: restaurants, schools, grocery stores, churches, gas stations, pharmacies and drug stores, banks, hospitals, parks, and shopping malls. We counted the number of POIs in each county and calculated their density as their facility distribution feature.
Road density
To capture the distribution of transportation network, we extracted data from Open Street Map51 to calculate the density of road segments in counties. We estimated complete road networks from the raw data by assembling road segments. Since the lengths of road segments created by the source were in close proximity, we calculated road density by dividing the number of road segments by the areas of a county.
Urban centrality index
We adopted UCI to characterize the centralization degree of the facilities in a county. UCI is the product of the local coefficient and the proximity index52. The local coefficient was computed based on the number of POIs within each census tract; the proximity index was computed based on the number of POIs within each census tract along with a distance matrix that considered the distance between census tracts. The value of UCI ranges from 0 to 1. The values close to 0 indicate polycentric distribution of facilities within a county, while the values close to 1 indicate monocentric distribution of facilities. The indices are formulated as follows52:
$${LC}=\frac{1}{2}\mathop{\sum }\limits_{i=1}^{N}({k}_{i}-\frac{1}{N})$$
(3)
$${PI}=1-\frac{V}{{V}_{\max }}$$
(4)
$$V={K}^{{\prime} }\times D\times K$$
(5)
where N is the total number of census tracts in a county; K is a vector of the number of POIs in each census tract; ki is a component of the vector K; D is the distance matrix between census tracts; Vmax is calculated by assuming that the total POIs are uniformly settling on the boundary of the county; LC is the local coefficient, which measures the unequal distribution; PI is the proximity index, which resolves the normalization issue; V is the Venables Index.
Human mobility index
To understand the inequality of population activities, we employed mobile phone data from Spectus Inc. to develop the metric of HMI. The data has a wide set of attributes, including anonymized user ID, latitude, longitude, POI ID, time of observation, and the dwelling time of each visit53. Prior studies found that Spectus mobile phone data is representative to describe human activities and mobility54,55,56. Hence, the feature generated using the dataset should be representative and valid for our analyses. We extracted the data from April 2019 (28 days) to account for the variation of population activities on weekdays and weekends. Our period is also during regular conditions when no external extreme events perturbed human activities. To develop the HMI, we first assigned each visit point \({v}_{i}\) to a defined CBG in a county. Then, we calculated HMI as follows:
$${HMI}=\frac{{\sum }_{i=1}^{n}{v}_{i}\,}{28n}$$
(6)
where n denotes the number of CBGs in a county.
We finally mapped the values of HMI to the range from 0 to 1 using min-max scaling. The proximity of HMI values to 0 or 1 indicates the level of human mobility and activity, with values closer to 0 indicating lower activity and values closer to 1 indicating higher activity in a county.
Statistical analysis
Ordinary least squares regression model
We employed an ordinary least squares regression model to capture the relationships between urban form and structure and spatial inequality of property flood risk among counties and to understand the relative importance of each feature57:
$${y}_{i}\sim {\beta }_{0}+{\beta }_{1}{x}_{i,1}+{\beta }_{2}{x}_{i,2}+{\beta }_{3}{x}_{i,3}+{\beta }_{4}{x}_{i,4} \\ + \, {\beta }_{5}{x}_{i,5}+{\beta }_{6}{x}_{i,6}+{\beta }_{7}{x}_{i,7}+{\beta }_{8}{x}_{i,8}+{\varepsilon }_{i}$$
(7)
where, yi is the SGI of county i; xi,1–xi,8 are the features of urban form and structure; β are coefficients; εi is the error term.
In the regression, since the values of POI density, population density, road density, and GDP have a much larger scale than other variables, we used logarithmic transformation of values. Three statistical tests, Kendall’s tau test, Pearson’s correlation test, and Spearman’s rank correlation test were then conducted for the correlation analyses to examine statistical significance and determine feature importance.
Classification and regression tree model
The CART model is an unsupervised machine learning algorithm used to build a decision tree by recursively splitting the data based on the predictor variables to minimize the entropy in the response variable58. The decision tree consists of a series of nodes, each representing a split in the data based on a particular predictor variable, and terminal nodes representing the predicted response variable for a given combination of predictor variable values. The method to identify the best splits is to minimize the entropy. If the entropy of the two child nodes is not lower than that of a parent node, splitting will be terminated any further. The entropy (E) is given by59:
$$E=-\mathop{\sum }\limits_{i=1}^{n}{p}_{i}{\log }_{2}({p}_{i})$$
(8)
where \({p}_{i}\) is the fraction of items in the class i.
In this study, we categorized the SGI into five levels: 0 to ≤20% (minor inequality), 20% to ≤40% (moderate inequality), 40% to ≤60% (major inequality), 60% to ≤80% (severe inequality), and 80% to ≤100% (extreme inequality). Then, we implemented a CART classification algorithm using the principal components as the predictor variables and SGI levels as the response variable.
Decision trees were utilized to pinpoint the factors that shape pathways to different levels of spatial inequality of property flood risk among different counties. By analyzing the decision trees and the pathways they present, this study aims to shed light on the contributing factors to the spatial inequality of property flood risk in the United States. Our primary objective is to uncover as many pathways as possible while maintaining good performance, considering the balance between complexity and performance. To achieve this, we set the minimum split leaf size to 100 counties and limit the tree depth to seven, enabling us to generate more pathways while also limiting the tree depth to prevent overfitting.
